Увлекательная ГЕОМЕТРИЯ
GeoGebra (Набор приложений, включая бесплатные инструменты для геометрии, таблицы, вероятности)
- поможет учителям для объяснения, а школьникам в ознакомлении с учебными материалами не только курса геометрии, но и алгебры, и математического анализа, будет незаменима в практиковании навыков и наглядном представлении.
и целый ряд команд, включая дифференцирование и интеграцию.
Можно СКАЧАТЬ GeoGebra и установить себе на компьютер или гаджет (нажмите Download в приложении). Как это делается, см. в видео ниже
Скриншоты:
Учебники GeoGebra Видео. Смотреть некоторые из GeoGebra Видео уроков, чтобы узнать, как использовать GeoGebra по различным темам математики
GeoGebra: обучающие видео на русском языке
GeoGebra: обучающие видео на английском языке
Далее Вы будете знакомиться к GeoGebra, исследуя три примера
Вы должны решить их один за другим и не забыть использовать данные подсказки
Пример 1: Окружности треугольникаПример 2: Касательные к окружности
Пример 3: Производная и касательная функции
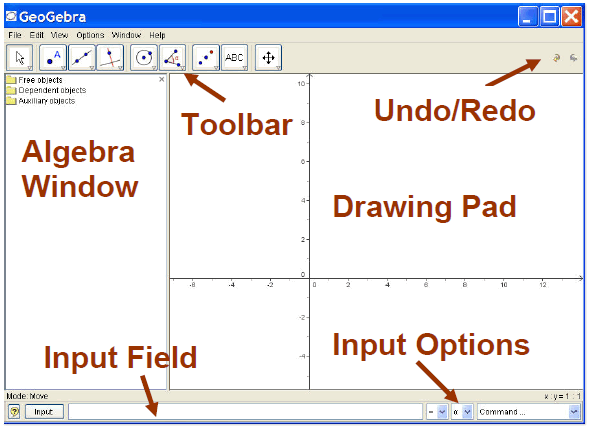
После старта GeoGebra появляется такое окно
Посредством панели инструментов toolbar Вы можете строить в окне для рисования drawing pad мышью. В то же самое время соответствующие координаты и уравнения будут показаны в окне алгебры algebra window. Входная текстовая область input text field используется для ввода координат, уравнений, команд и функций соответственно, Input Field - поле ввода, Input Options - параметры ввода; они немедленно отображаются на чертеже, т.е. в блокноте-окне для рисования после нажатия клавиши ENTER. Геометрия и алгебра бок о бок:
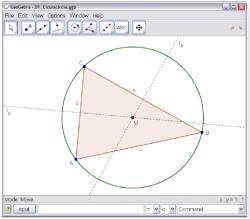
Пример 1: Построение окружности вокруг треугольника
Задача: Построить окружность вокруг треугольника A, B, C с использованием GeoGebra
Построить с помощью мыши.
 Выберите режим "Многоугольник” на панели инструментов (нажмите на маленькую стрелку - третий значок слева). Теперь нажмите на окно для рисования три раза, чтобы создать вершины A, B и C. Завершите построение треугольника, нажав на вершину А еще раз.
Выберите режим "Многоугольник” на панели инструментов (нажмите на маленькую стрелку - третий значок слева). Теперь нажмите на окно для рисования три раза, чтобы создать вершины A, B и C. Завершите построение треугольника, нажав на вершину А еще раз.
Затем выберите режим "Серединный перпендикуляр" и постройте два серединных перпендикуляра, нажав на две стороны треугольника.
 В режиме "Пересечение двух объектов" вы можете нажать на пересечение двух серединных перпендикуляров, чтобы получить центр окружности. Назовем эту точку "М", для этого щелкните по ней правой кнопкой мыши (Mac OS: Ctrl-клик) и выберите (переименовать) в появившемся меню.
В режиме "Пересечение двух объектов" вы можете нажать на пересечение двух серединных перпендикуляров, чтобы получить центр окружности. Назовем эту точку "М", для этого щелкните по ней правой кнопкой мыши (Mac OS: Ctrl-клик) и выберите (переименовать) в появившемся меню. Чтобы закончить построение, вы должны выбрать режим "окружность по центру и точке" и нажать сначала в центр, затем на любую вершину треугольника.
Чтобы закончить построение, вы должны выбрать режим "окружность по центру и точке" и нажать сначала в центр, затем на любую вершину треугольника. Теперь выберите режим "Перемещение" и используя мышь, можете изменить положение любой из вершин - вы поймете смысл "динамической геометрии".
Теперь выберите режим "Перемещение" и используя мышь, можете изменить положение любой из вершин - вы поймете смысл "динамической геометрии".Некоторые советы:
Попробуйте использовать значок "Отмена" на правой стороне панели инструментов.
Чтобы скрыть объект, щелкните правой кнопкой мыши на нем (Mac OS: Ctrl-клик) и снимите флажок "Показать объект".
Свойства объектов (цвет, тип линии, ...) могут быть легко изменены: правой кнопкой мыши (Mac OS: Ctrl-клик) снова нажмите на объект и выберите "Properties” "Свойства" в появившемся контекстном меню.
В меню "Вид" окна алгебры оси и сетки могут быть скрыты или показаны.
Для того чтобы изменить положение окна для рисования, выберите режим "Переместить чертеж" (последний значок панели инструментов) и просто используйте мышь для перемещения.
Меню "Вид - Протокол" предоставляет таблицу с указанием всех шагов, которые вы предприняли при построении чертежа. Это позволяет повторить все построение шаг за шагом с помощью клавиш со стрелками, а также можно изменить порядок различных шагов.
Кроме того, вы можете использовать меню "Вид", чтобы скрыть или показать нежелательные колонки.
Дополнительная информация о построении с помощью мыши можно найти в меню "Справка", раздел "Geometric input”.
Использование для построения текстового поля ввода.
Сейчас мы собираемся сделать то же самое построение, используя текстовое поле ввода.
Вам потребуется новая площадка для рисования (меню "Файл - Создать"). Затем введите следующие команды в поле ввода текста в нижней части экрана, нажимая клавишу ввода Enter после каждой строки:
A = (2, 1)Дополнительные советы:
B = (12, 5)
C = (8, 11)
Polygon[A, B, C]
l_a = LineBisector[a]
l_b = LineBisector[b]
M = Intersect[l_a, l_b]
Circle[M, A]
Автоматическое завершение команды: после ввода первых двух букв команды, она будет отображаться автоматически. Если вы хотите принять предложенную команду, нажмите enter, иначе просто продолжайте печатать.
Это не является необходимым для ввода каждой команды, вы можете также выбрать ее из списка команд, что находится в непосредственной близости от поля ввода текста.
Нажатие на икону "Ввод" (внизу слева) активирует режим "Поле ввода". В этом режиме вы можете нажать правой кнопкой мыши на объект из окна алгебры или окна для рисования, чтобы скопировать его в поле ввода текста.
Дополнительные советы, касающиеся текстового поля ввода: нажмите на знак вопроса в левом углу.
Вы получите особенно хорошие результаты от работы с GeoGebra путем объединения преимуществ обеих форм ввода, мышью и текстового поля ввода.
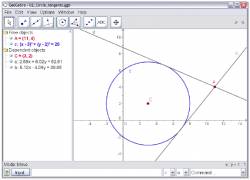
Пример 2: Касательные к окружности
Задача: Использовуя GeoGebra, построить окружность с: (х - 3) ² + (у - 2) ² = 25 и ее касательные через точку = (11, 4)
Использование для построения поля ввода текста и мыши.
Вставьте уравнение окружности c: (x - 3)² + (y - 2)² = 25 в поле ввода текста и нажмите клавишу ввода (показатель может быть найден в списке справа в поле ввода)
Введите команду C = Center[c] в поле ввода текста.
Постройте точку А с координатами = (11, 4).
 Теперь выберите режим "касательные" и нажмите на точку А и окружность С.
Теперь выберите режим "касательные" и нажмите на точку А и окружность С. После выбора режима "Переместить", перетащите точку А с помощью мыши и наблюдайте движение касательных.
После выбора режима "Переместить", перетащите точку А с помощью мыши и наблюдайте движение касательных.Также попробуйте переместить окружность С и посмотреть на ее уравнение в окне алгебры.
Некоторые советы:
Можно использовать инструменты в правом меню панели инструментов, чтобы увеличить или уменьшить масштаб (кликните правой кнопкой мышки). Если у вас мышь с колесиком, попробуйте использовать Ctrl + колесо мыши для увеличения.
Можно изменить уравнение окружности непосредственно в окне алгебры дважды щелкнув по нему мышью.
Более подробную информацию о возможностях поля ввода текста можно найти меню "Справка", раздел "Algebraic input".
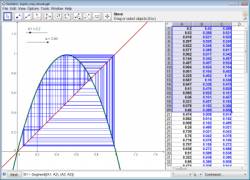
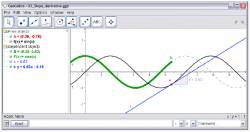
Пример 3: Производная и касательная функции
Задача: Используйте GeoGebra, чтобы построить функцию f(x) = sin(x), её производную и касательную в точке функции f, плюс наклон треугольника (касательной). Версия 1: Точка на функции
Вставьте функцию f(x) = sin(x) в поле ввода текста и нажмите клавишу ввода enter.

Выберите режим "точка" и нажмите на функцию f. Это создаст точку A на f.
 Затем выберите режим "касательные" и нажмите на точку А и функцию f.
Затем выберите режим "касательные" и нажмите на точку А и функцию f.Изменените имя касательной на t (правой кнопкой мыши (Mac OS: Ctrl-клик), "переименовать").
Следующая команда s = наклон[t] показывает наклон касательной.
 После выбора режима "Перемещение", перетащите точку А с помощью мыши и наблюдайте движение касательной.
После выбора режима "Перемещение", перетащите точку А с помощью мыши и наблюдайте движение касательной.Введите команду B = (x(A), s) и перейти на след этой точки (нажмите на B правой кнопкой мыши (Mac OS: Ctrl-клик) и выберите "оставлять след".) x(A) дает вам координаты х точки А.
 Выберите режим "Перемещение" и перетащите А с помощью мыши - B оставит след.
Выберите режим "Перемещение" и перетащите А с помощью мыши - B оставит след.Последняя команда Производная[f]
Получаем производную [f] - [f]'
Советы:
Вставьте различные функции, например, f(x) = x³ - 2x² в поле ввода текста; сразу ее производная и касательная будут отображаться.
Выберите режим "Перемещение" и перетащите функции графика с помощью мыши. Наблюдайте изменение уравнения функции и ее производной.
Версия 2: точка x = a
Сейчас мы собираемся сделать еще один вариант последнего построения. Поэтому, выбирайте "Файл - Создать", чтобы получить новую площадку для рисования. Далее, введите следующие команды в текстовое поле ввода и нажимайте клавишу ввода Enter после каждой строки.
f(x) = sin(x)
a = 2
T = (a, f(a))
t = Касательная[a, f]
s = наклон[t]
B = (x(T), s)
Производная[f]
Выберите режим "Переместить" и нажмите на число a в левом окошке. Вы можете изменять его, нажимая на клавиши со стрелками. В то же время, точка Т и касательная будут двигаться по функции f.
Вы также можете изменять значение числа а с помощью ползунка: для этого в окне алгебры надо выбрать мышкой число а и в окне для рисования, щелкнув правой кнопкой мыши (Mac OS: ctrl-click), выбрать "Показать объект".
Совет: ползунки, а также клавиши со стрелками, очень полезны для изучения параметров p и q в квадратных уравнениях y = x² + px + q
Касательные без данной команды
GeoGebra в состоянии иметь дело с векторами, а также параметрическим представлением линий.
Поэтому можно построить касательную t без команды "Касательная []". Чтобы убедиться в этом, удалите касательную с вашего чертежа, щелкнув по нему правой кнопкой мыши (Mac OS: Ctrl-клик) и выбрав пункт "Удалить". Затем введите следующие команды:
v = (1, f'(a))
t: X = T + r v
v это направление вектора касательной t. Вместо r вы можете также использовать любое другое буквенное обозначение в качестве параметра.
Существует дополнительная возможность для построения касательной с помощью направляющего вектора: t = Line[T, v].
Также попробуйте команду интеграл[f]